BÀI GIẢNG: MA TRẬN VÀ ỨNG DỤNG
1. Khái nim Ma trận
Ma trận là một bảng số hình chữ nhật gồm ![]() hàng và
hàng và ![]() cột. Ký hiệu tổng quát:
cột. Ký hiệu tổng quát: ![]() .
.
Ví dụ minh họa:
Xét ma trận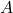 cấp
cấp  :
:
Xét ma trận
![]()
- Phần tử nằm ở hàng 2, cột 1 là
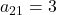 .
. - Phần tử nằm ở hàng 1, cột 2 là
 .
.
2. Các phép toán với Ma trận
a. Phép cộng hai ma trận
Điều kiện: Hai ma trận phải cùng kích thước. Ta cộng các phần tử ở vị trí tương ứng: ![]() .
.
Ví dụ:
![]()
b. Phép nhân ma trận với một số
Nhân số ![]() vào tất cả các phần tử của ma trận.
vào tất cả các phần tử của ma trận.
Ví dụ (với k=3):
![]()
c. Phép nhân hai ma trận
Điều kiện: Số cột của ma trận trước bằng số hàng của ma trận sau. Phần tử ![]() là tích vô hướng của hàng
là tích vô hướng của hàng ![]() ma trận trước với cột
ma trận trước với cột ![]() ma trận sau.
ma trận sau.
Ví dụ:
![]()
3. Định thức (Determinant)
Định thức là con số đặc trưng cho ma trận vuông, ký hiệu ![]() hoặc
hoặc ![]() .
.
Trường hợp cấp 2 (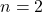 )
)
Công thức: ![]() .
.
Ví dụ:
![]()
Trường hợp cấp 3 ( )
)
Sử dụng quy tắc Sarrus hoặc khai triển Laplace (theo hàng/cột chứa nhiều số 0).
Ví dụ (Khai triển theo cột 1):
Cho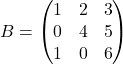
Cho
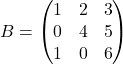
![]()
![]()
4. Ma trận nghịch đảo
Ma trận vuông ![]() có nghịch đảo
có nghịch đảo ![]() khi
khi ![]() .
.
Công thức cấp 2: ![]()
Ví dụ: Tìm 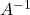 của
của 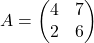 .
.
1. Tính định thức: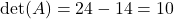 .
.
2. Áp dụng công thức:
1. Tính định thức:
2. Áp dụng công thức:
![]()
5. Giá trị riêng và Ứng dụng
Giá trị riêng ![]() là nghiệm của phương trình đặc trưng:
là nghiệm của phương trình đặc trưng: ![]() .
.
Ví dụ tính toán (với 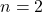 ):
):
Cho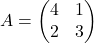 .
.
PT đặc trưng: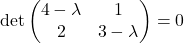
Cho
PT đặc trưng:
![]()
![]()
Giải ra ta được: ![]() .
.
Ứng dụng thực tiễn:
- Cơ học: Tính toán tần số dao động riêng (tránh cộng hưởng cầu, cánh máy bay).
- CNTT: Thuật toán Google PageRank, nén ảnh, nhận diện khuôn mặt.
